|
|
|
PREDICTING SOLUTE DISTRIBUTION WITH CONVECTIVE-DISPERSIVE APPROACH
Increasing concern about the
presence of pesticides and other agricultural chemicals as potential groundwater
pollutants has led to strict regulation of their use, and in particular
on their concentration levels allowable in ground water. Water is nature’s
primary vehicle for the transport of dissolved chemicals and methods for
analyzing the movement and fate of pesticides in the soil to minimize
the risks of ground-water contamination have to be developed. Most of
conventional transport models developed are based on the convective-dispersive
equation which, in most formulations, assumes that water and solutes follow
an average path through the soil-which is to say that a given molecule,
starting at the surface, is equally likely to follow any one of a multitude
of available paths.
The approach used by many soil
scientists to simulate water and solute flow in unsaturated soils is based
on a theory derived by L.A. Richards in 1931. In 1956 Wiebe vand der Molen
combined aspects of this model with the the theory of dispersive movement
to predict the course of desalinization of land in the Netherlands that
had been inundated by seawater. The resulting convective-dispersive equation
assumes that water and solutes follow an average path through the soil-
which is to say that a given molecule, starting at the surface, is equally
likely to follow any one of a multitude of available paths.
Typical of models based on
the convective-dispersive equation is MOUSE (Model of Underground Solute
Evaluation) developed by Steenhuis et. al. in 1987. MOUSE and similar
models have proven quite satisfactory for predicting the overall flow
of water and the transport of nitrates. In studies conducted on Long Island,
the predicted values are acceptably close to values determined by sampling
(Figures 1 and 2). But studies of pesticides conducted at similar sites
failed to predict the speed with which the contaminants penetrated the
soil (Figure 3). This failure occurs because the models are unable to
predict spatial and temporal variations of pesticide concentration sometimes
found in the groundwater. The models does not consider preferential flow
paths through which the solute can quickly bypass the biologically active
root zone and thereby reduce the potential for degradation.
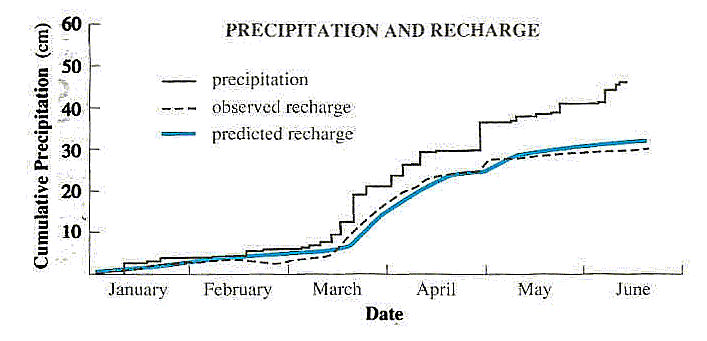
Figure 1. Precipitation
and recharge
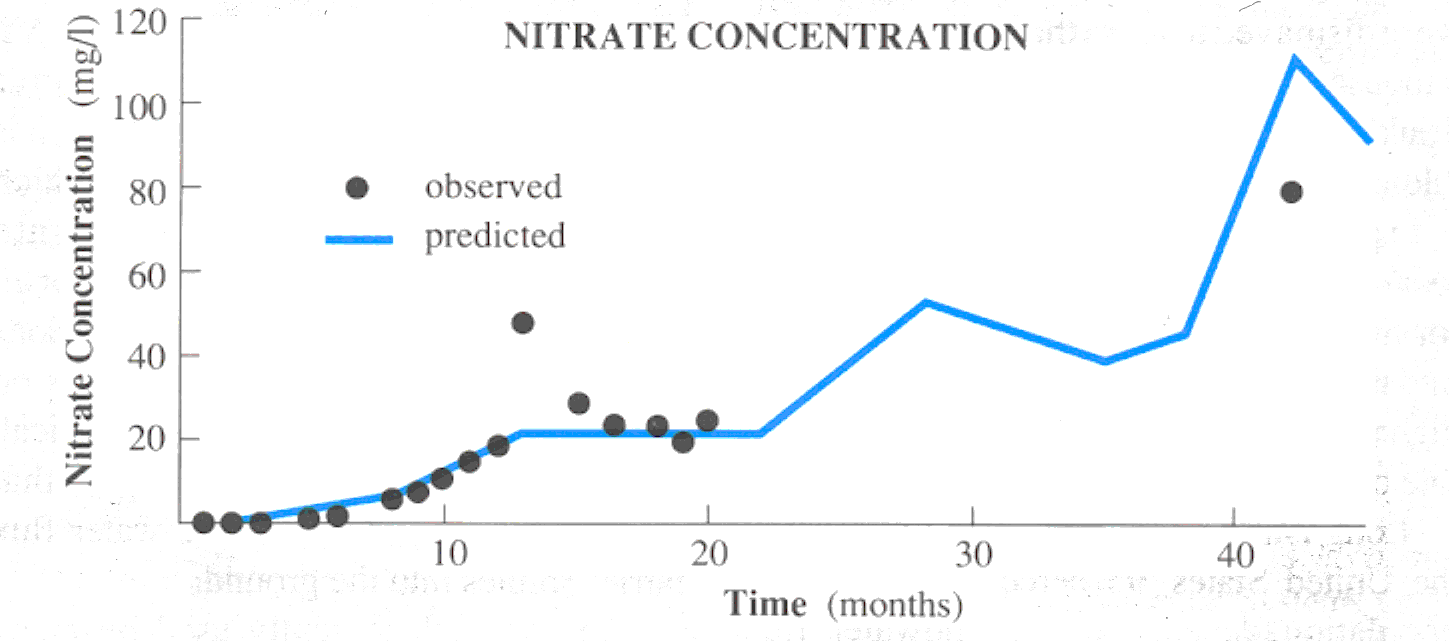
Figure 2. Nitrate
concentration
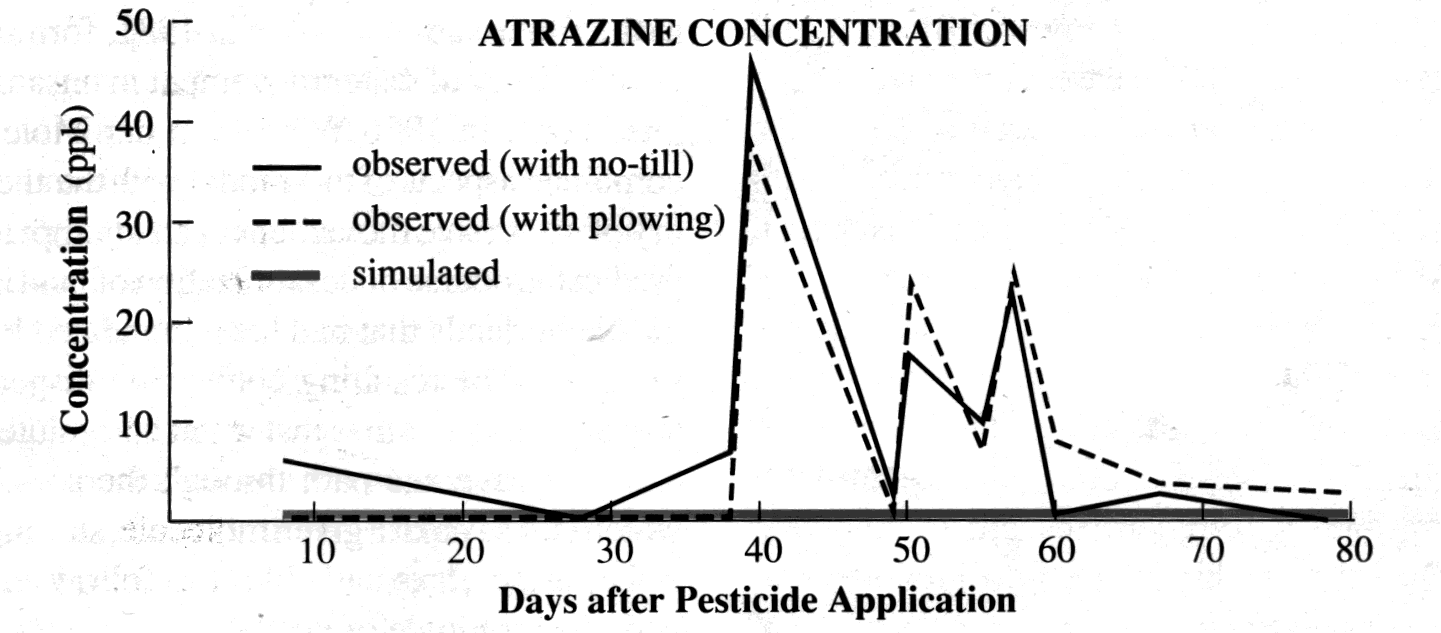
Figure 3. Atrazine
concentration
The difference in predictive
accuracy between the pesticides, on one hand, and nutrient and water,
on the other hand, results, in part, in a wide disparity in the amount
of chemicals that will cause health standards to be exceeded. According
to limits set by the Environmental Protection Agency, nitrates are tolerable
in concentrations up to 10,000 parts per billion, which are not attained
unless more than 40% of the amount commonly applied reaches groundwater.
In contrast, the maximum permissible pesticide concentration is usually
below 10 parts per billion. On Long Island, a concentration of 2.5 parts
per billion may be attained if just one quarter of one percent of the
amount usually applied reaches groundwater. Since this limit can be exceeded
if only a small amount of solute follows a non-average flow path, averaging
models based on the convective-dispersive equation are too simplistic.
A more sophisticated model must be developed to recognize that water does
not infiltrate the soil uniformly, but shows a preference for certain
pathways such as wormholes, cracks, structural faults or fractures, animal
burrows, sub-surface erosion, root holes, etc; resulting in much faster
transport of pesticides, and other contaminants, including nutrients,
trace metals, and manurial pathogens.
Preferential Flow
|

